Filtering
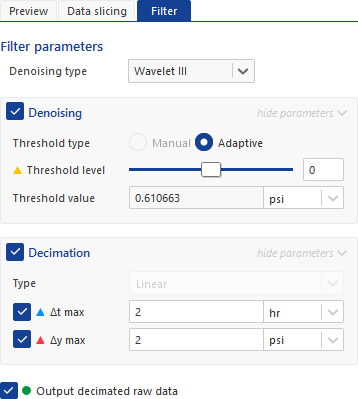
In order to reduce the size of raw time series data, KAPPA-Automate applies denoising and decimation techniques. This involves applying a signal processing technique to identify/sketch a distinct trend in the time series data with inherent noise. The diagram below illustrates an identified trend (orange dots) and the raw data with inherent noise (gray dots).
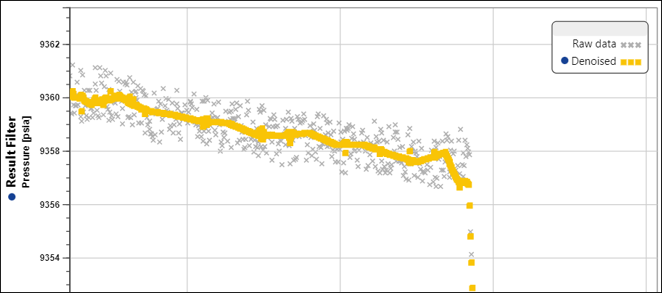
While denoising squeezes the data points into a representative data trend, it does not reduce their number. In order to reduce the number of data points a decimation technique is applied to the denoised data trend. This technique produces a smaller subset of points to represent the data trend. The red and blue dots in diagram below illustrate how denoised data is decimated.
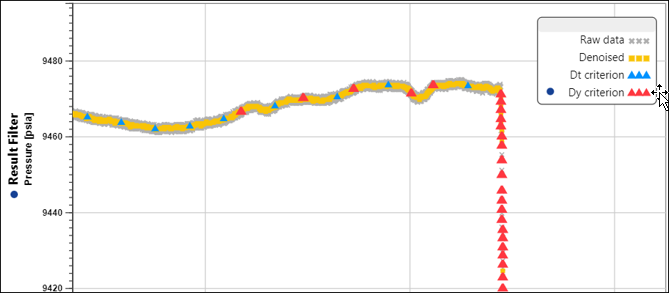
Denoising and decimation function together to identify the data trend and represent it with a fewer number of points by filtering out redundant and/or noisy data. This approach preserves characteristic features such as shut-ins and at the same time reduces the number of points from millions to a manageable size of thousands.
Three main versions of denoising algorithms are available in KAPPA-Automate. The integral filter is another method of filtering.
During the decimation process, it is possible to specify the number of points to retain from the de-noised data. This is set by specifying the “Delta-T max” and/or “Delta-Y max” criteria: one point every Delta-t max, with Delta-y value less than Delta-y max;
∆t max — maximum time between points if the 'delta y' value for them is less than the delta max. Default value set to 2 hours.
∆y max — maximum 'delta y' value between consecutive points. For rates data 'delta y' max is set to 10 stb/d, for pressure data delta y max is set to max (2psi, threshold value).
Output Decimated Raw Data — This option is only available with the Wavelet II denoising algorithm. When set, the Filter process creates an additional filtered data set with raw data points, i.e. the data points retain their original values without any changes due to the denoising algorithm.
This algorithm of denoising requires that the data points are evenly spaced. Prior to applying the algorithm, data is resampled at equal intervals. Denoising is then performed on the resampled evenly spaced data. This method is sensitive to data with large gap duration's due to the resampling approach as artificial data points can be created by data interpolation. Therefore, it is advisable to adequately set the minimum gap duration to exclude sections with no data points.
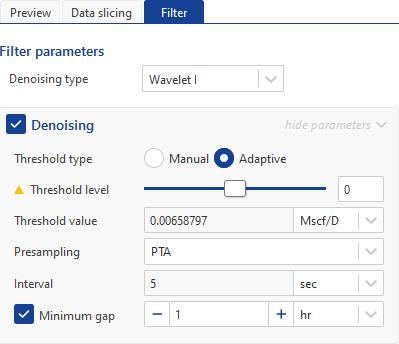
Presampling — This option is accessible only with Wavelet I denoising. Three preset values and a user defined option are available. As a rule, it is not advisable to resample data with a higher frequency than the acquisition frequency of the raw gauge data due to the creation of artificial data points.
PTA — is suitable if the filtered data is primarily targeted for pressure transient analysis. This method sets resampling time to 1 second, however if the min time between real data points is more than 1 second then the later will applied. This serves as a guard against generating large numbers of artificial data points in cases when the raw gauge data was acquired with a much lower sampling frequency.
Intermediate — This method is applicable for cases when the filtered dataset is used for both pressure transient analysis and production analysis. The resampling interval in this case is set to 15 seconds.
PA — In cases where the filtered data is considered only for production analysis the 5-minute interval best serves this purpose.
User — This setting allows the user to manually set any custom resampling time.
Minimum Gap — The minimum gap duration option defines the minimum time interval between two consecutive data points for them to be regarded as a continuous stream of data. Any gap that exceeds this interval is considered as absent data. This setting is used in Wavelet I denoising algorithm. Time gaps that exceed this value will not be interpolated with extra data points.
Wavelet II denoising algorithm does not require resampling of data with a constant time interval. It performs the denoising procedure directly using available data points. With this approach there is no interpolation step to create artificial data points. This algorithm also ignores the minimum gap.
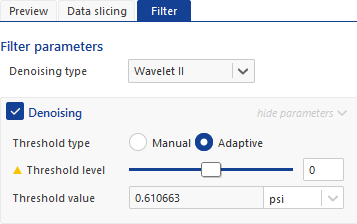
Threshold Type — This is an internally calculated (or explicitly set by a user) noise level for a pre-loaded data slice. The threshold is applied to high frequency data points in the denoising process. The value is internally calculated from a pre-loaded data slice when a user navigates to the filter tab. KAPPA-Automate supports two different modes of calculating thresholds in the denoising process.
Manual — An initial threshold value is automatically calculated from a data slice selected at the pre-load stage. This same value is then applied to all the data during the denoising process. This works well if the dataset has almost a constant noise level throughout its history. Users can manually change the fixed threshold value directly by typing the required value.
Adaptive — In this mode KAPPA-Automate calculates a threshold value for each data slice separately and applies it in the denoising algorithm. Threshold values in adaptive mode are adjusted only by using the Threshold level slide bar. The Threshold level serves as a boost factor that is equally applied to all threshold values internally calculated from pre-loaded data slices.
Threshold Level — A Threshold level slide bar is a user interface control device that is used to set a general boost factor applicable to all the automatically calculated threshold values in the adaptive mode. Threshold levels range from +100 to -100. The boost factor value is applied to threshold values using the formula below. It is important to note that manually setting the threshold value (Sigma final) in fixed mode initiates a re-estimation of the initially calculated threshold (Sigma I) using the current filter level. Irrespective of the threshold mode used, only the Sigma final parameter is passed to the denoising procedure.
σfinal = σi x 10L/50
where,
σfinal - threshold value used in the denoising algorithm
σi - initially calculated threshold
L - filter level
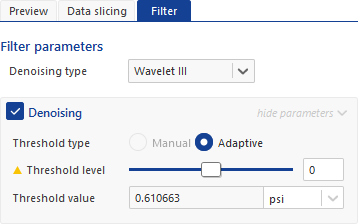
The Wavelet III denoising algorithm is a less memory-intensive and more efficient implementation of the Wavelet II algorithm. Only adaptive thresholding is available for the Wavelet III option.
The integral filter is available for rate data only. The algorithm is designed to respect the cumulative production over time. It aggregates time steps and tracks cumulative production over time given user-specified constraints on cumulative production, changes in flow rates, and elapsed time. Rate values are chosen to respect the cumulative production. In addition, the algorithm records explicitly the start and end times of shut-ins.
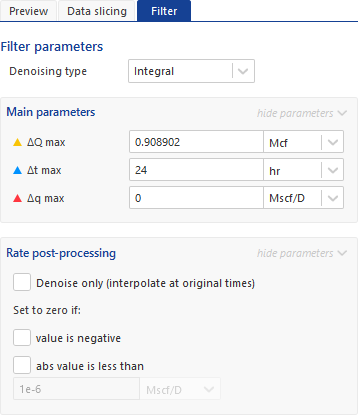
The following parameters control the filter setup:
∆Q max — Maximum cumulative production between decimated points – Ensures that periods of high-rate changes have higher resolution in time.
∆t max — Maximum time elapsed between decimated points — Ensures a certain time resolution.
∆q max — Maximum rate change — Can capture transients.
Technical References
KAPPA DDA Book, Chapter 16 — Permanent Gauges & amp: Intelligent Fields
SPE 139216: "New Methods Enhance the Processing of Permanent Gauge Data"